Dimensionality reduction and ordinations in ecology 2: Principal Component Analysis (PCA)
Since principal component analysis (PCA) is the most basic and commonly used dimensionality reduction method, I would like to explain some basis to understand PCA used in ecological research.
As analysis of variance (ANOVA) can decompose total variance into variances explained by factors and error, PCA attempts to find new axes to explain the most variability of your multivariate data.
Let us assume that your data has 100 variables for each observation. Say one forest site has 100 species abundances or one chromatogram has 100 peak areas. If you want to compare your observations and to find ecological patterns, you need to plot 100-d space with 100 axes, which is only possible in mathematical world. In mathematics, you can produce N-dimensional hypervolume such as Hutchison' niche concept (Hutchinson 1957). However, it is hard to visualize 100-d space. If we can reduce 100-d data into 2 or 3-d data, we can visualize your data in 2-d or 3-d space. That is dimensionality reduction and my previous post explains its overall concept.
PCA attempts reduce dimensionality of your multivariate data by replacing new axes in the order of variability explained. PCA produce 100 new axes from the original 100 variables by linear algebric conversion.
Since 100 d data is difficult to visualize, let us have 3 d dataset for explanation of PCA. PCA attempts to find an axis which explains the most variability like a regression line. The first axis explains the most variability of the original dataset.
This axis is called the first principal component (PC1) axis. Actually, PC1 is an eigenvector in linear algebra. In similar way, you can find the second axis which explains the most variability on the residuals. This second axis is called the second principal component (PC2). Since, the number of variables in the original dataset is 3, the number of the converted principal component should be 3. Therefore, PCA should produce PC3, too. PCA produce n new principal components from n original variables. What is the differences between the old axes (variables) and the new principal component? Principal components are numbered by their importances (how much they explain the total variability), which is related to their eigenvalues. In PCA, PCs with low component number would always have higher eigenvalues like Fig. 2.
If you calculate the percentage of each eigenvalue to the total sum of all eigenvalues, you can get variances explained by each principal component like Table 1.
In Table 1, the first two principal components explain 84.1% of the total variance. This is the beauty of PCA logic. PCA transforms your multivariate data with N variables into n new axes (PCs) in order of higher eigenvalues through linear transformation (linear algebra). Even though you have same number of new axes (PCs), you can explain 84.1% of the total variance of the original data with only the first 2 axes (PC1 and PC2). This is how PCA reduce dimensionality of your multivariate data.
Fig. 2 shows typical PCA results from 40 individuals of an endangered plant species regarding 14 variables with moisture (M0, M1, M2, M3) and nutrient treatments (N0, N1, N2, N3). The plot indicate that Factor 1 (PC1) explains 37.8% of the total variance while Factor 2 (PC2) explains 29.6%. Both PC1 and PC2 explain 66.6%, that is almost 2/3 of the total variance of the original dataset. The authors interpret that N3 (high nutrient treatment) made differences from the other treatment. Those individuals under N3 shows scores negative on both PC1 and PC2. Since PC1 and PC2 are new axes made of weighted calculation of the original 14 variables, you may want to look further on the meaning of PC1 and PC2. One way to find the meaning of PCs would be correlation of original variables with PCs such as Table 2 below.
An another way to find meanings of PCs is analyzing loading values for important PCs. What is loadings? It is weights or coefficients of the original variables in making a PC.
Let us look at PCA's mathematical expression.
where C1 is a score of an observation on PC1, b1p is a weight (loading) of variable p, and Xp is an original score of variable p. Don't worry, I will show you a graphical way of this.
Each observation would have new score on each PC. One observation would have two scores from PC1 and PC2, which can be used two coordinates in PC1-PC2 plane. If you use three PCs, you can use 3 scores from PC1, PC2, and PC3 for x,y,z coordinates in 3-d space.
From above, you can understand that loading values are weights of original variables in producing PCs. If you recognize PC1 shows meaningful clustering, take a look at loadings for PC1 to find important variables.
Let us examine the sesarmid crab example (Yang et al. 2019) mentioned in the previous post again (Fig. 4). In this PCA scoreplot on crab fatty acid compositions, crabs of smaller size groups (I and II) and crabs of larger size groups (III and IV) are clustered along PC2 regardless of sites. You may ask which fatty acids contributed most to the differences between smaller crabs and larger crabs.
Since scores of the larger size crabs appear to be relatively positive on PC2, you might consider loadings for PC2. For explanation purpose, I made an imaginary loading plots for the scoreplot above as follows:
Now you may understand why Yang et al. (2019) state as follows:
"Specifically, the FA content of 18:3ω3, a biomarker of plant materials (Dalsgaard et al. 2003), was a major factor to separate size groups based on PCA loadings, indicating that the plant diet might make an important difference in the feeding by different-sized crabs (data not shown)."
By Sangkyu Park (Editor-in-Cheif of Journal of Ecology and Environment)
References
(1957) Concluding remarks. Cold Spring Harbor Symposia on Quantitative Biology, 22, 415–427.
Lee E-P (2017) Effect of nutrient and moisture on the growth and reproduction of Epilobium hirsutum L., an endangered plant. Journal of Ecology and Environment (2017) 41:35.
Yang et al. (2019) Intraspecific diet shifts of the sesarmid crab, Sesarma dehaani, in three wetlands in the Han River estuary, South Korea. Journal of Ecology and Environment, 2019 43:6.
Scholz M (2006) Approaches to analyse and interpret biological profile data. Dissertation. Max Planck Institute of Molecular Plant Physiology Bioinformatics Group
As analysis of variance (ANOVA) can decompose total variance into variances explained by factors and error, PCA attempts to find new axes to explain the most variability of your multivariate data.
Let us assume that your data has 100 variables for each observation. Say one forest site has 100 species abundances or one chromatogram has 100 peak areas. If you want to compare your observations and to find ecological patterns, you need to plot 100-d space with 100 axes, which is only possible in mathematical world. In mathematics, you can produce N-dimensional hypervolume such as Hutchison' niche concept (Hutchinson 1957). However, it is hard to visualize 100-d space. If we can reduce 100-d data into 2 or 3-d data, we can visualize your data in 2-d or 3-d space. That is dimensionality reduction and my previous post explains its overall concept.
PCA attempts reduce dimensionality of your multivariate data by replacing new axes in the order of variability explained. PCA produce 100 new axes from the original 100 variables by linear algebric conversion.
Since 100 d data is difficult to visualize, let us have 3 d dataset for explanation of PCA. PCA attempts to find an axis which explains the most variability like a regression line. The first axis explains the most variability of the original dataset.
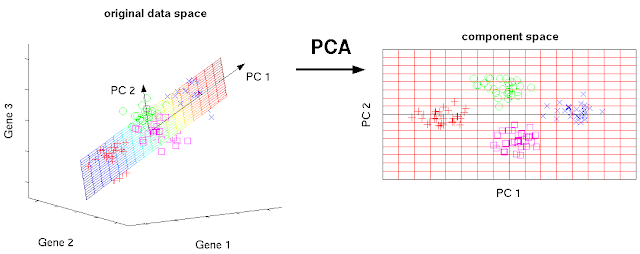 |
| Fig. 1 PCA convert original axes into new axes which explain the most variabilities (c) Matthias Scholz Ph.D. Dissertation CC BY 2.0 DE license |
This axis is called the first principal component (PC1) axis. Actually, PC1 is an eigenvector in linear algebra. In similar way, you can find the second axis which explains the most variability on the residuals. This second axis is called the second principal component (PC2). Since, the number of variables in the original dataset is 3, the number of the converted principal component should be 3. Therefore, PCA should produce PC3, too. PCA produce n new principal components from n original variables. What is the differences between the old axes (variables) and the new principal component? Principal components are numbered by their importances (how much they explain the total variability), which is related to their eigenvalues. In PCA, PCs with low component number would always have higher eigenvalues like Fig. 2.
 |
| Fig.2 Eigenvalues of each principal componens. (c) Staticshakedown CC BY-SA 4.0 Source: https://en.m.wikipedia.org/wiki/File:Screeplotr.png |
If you calculate the percentage of each eigenvalue to the total sum of all eigenvalues, you can get variances explained by each principal component like Table 1.
 |
| Table 1. Eigenvalues and total variance explained (c) Philipendula GNU Free Documentation License. Source: https://commons.wikimedia.org/wiki/File:Allvariables.png |
In Table 1, the first two principal components explain 84.1% of the total variance. This is the beauty of PCA logic. PCA transforms your multivariate data with N variables into n new axes (PCs) in order of higher eigenvalues through linear transformation (linear algebra). Even though you have same number of new axes (PCs), you can explain 84.1% of the total variance of the original data with only the first 2 axes (PC1 and PC2). This is how PCA reduce dimensionality of your multivariate data.
 |
| Fig. 2. PCA scoreplot of 40 individuals of Epilobium hirsutum L. using 14 variables treated to moisture and nutrient gradients (M0-M3 for moisture treatment, N0-N3 for nutrient treatment). Lee E-P et al. Journal of Ecology and Environment (2017) 41:35. |
Fig. 2 shows typical PCA results from 40 individuals of an endangered plant species regarding 14 variables with moisture (M0, M1, M2, M3) and nutrient treatments (N0, N1, N2, N3). The plot indicate that Factor 1 (PC1) explains 37.8% of the total variance while Factor 2 (PC2) explains 29.6%. Both PC1 and PC2 explain 66.6%, that is almost 2/3 of the total variance of the original dataset. The authors interpret that N3 (high nutrient treatment) made differences from the other treatment. Those individuals under N3 shows scores negative on both PC1 and PC2. Since PC1 and PC2 are new axes made of weighted calculation of the original 14 variables, you may want to look further on the meaning of PC1 and PC2. One way to find the meaning of PCs would be correlation of original variables with PCs such as Table 2 below.
 |
| Table 2. Correlation matrix of 14 variables with the first and two principal component scores of PCA analysis. Lee E-P et al. Journal of Ecology and Environment (2017) 41:35. |
An another way to find meanings of PCs is analyzing loading values for important PCs. What is loadings? It is weights or coefficients of the original variables in making a PC.
Let us look at PCA's mathematical expression.
where C1 is a score of an observation on PC1, b1p is a weight (loading) of variable p, and Xp is an original score of variable p. Don't worry, I will show you a graphical way of this.
 |
| Fig. 3 Calculating scores of m observations on PC1. (c) S Park. |
From above, you can understand that loading values are weights of original variables in producing PCs. If you recognize PC1 shows meaningful clustering, take a look at loadings for PC1 to find important variables.
Let us examine the sesarmid crab example (Yang et al. 2019) mentioned in the previous post again (Fig. 4). In this PCA scoreplot on crab fatty acid compositions, crabs of smaller size groups (I and II) and crabs of larger size groups (III and IV) are clustered along PC2 regardless of sites. You may ask which fatty acids contributed most to the differences between smaller crabs and larger crabs.
 |
| Fig. 4. A score plot of PCA on fatty acid composition of sesarmid crab, Sesarma dehaani in three different wetlands along salinity gradient in Han River estuary, Korea. Source: Yang DW et al. Journal of Ecology and Environment, 2019 43:6 |
 |
| Fig. 5. A hypothetical loading results made for an explanation purpose. |
If Fig. 5 is the loading values from the above PCA scoreplot (Fig. 4), you would like to find out the strongest loadings on the second principal component (Comp.2) in Fig. 5. Since this loading plot shows loading values in the order of absolute values, the first original variable to the left has the strongest weight in calculating the second principal component (Comp.2). You will find that It is V19 with big positive loading values. Let us assume that the original variable V19 is 18:3ω3, you may interpret that 18:3ω3 concentrations would increase along Comp.2 since the loading value for V19 is positive. Along Comp.2, crabs in larger size groups (III and IV) have relatively positive scores, you may interpret that larger crabs have higher 18:3ω3 (biomarker for plant) indicating that larger crabs would feed more plant material.
"Specifically, the FA content of 18:3ω3, a biomarker of plant materials (Dalsgaard et al. 2003), was a major factor to separate size groups based on PCA loadings, indicating that the plant diet might make an important difference in the feeding by different-sized crabs (data not shown)."
By Sangkyu Park (Editor-in-Cheif of Journal of Ecology and Environment)
References
(1957) Concluding remarks. Cold Spring Harbor Symposia on Quantitative Biology, 22, 415–427.
Lee E-P (2017) Effect of nutrient and moisture on the growth and reproduction of Epilobium hirsutum L., an endangered plant. Journal of Ecology and Environment (2017) 41:35.
Yang et al. (2019) Intraspecific diet shifts of the sesarmid crab, Sesarma dehaani, in three wetlands in the Han River estuary, South Korea. Journal of Ecology and Environment, 2019 43:6.
Scholz M (2006) Approaches to analyse and interpret biological profile data. Dissertation. Max Planck Institute of Molecular Plant Physiology Bioinformatics Group
Comments
Post a Comment